Pročitajte razne zanimljivosti iz sveta matematike
Da li ste znali da se u matematici kriju mnoge zanimljivosti? O njenim brojevima, znacima, simbolima, teoremama i naučnicima postoji mnoštvo anegdota i zanimljivih činjenica. Začudićete se kako neke od njih do sada niste znali i koiko je matematika zapravo jedna životna nauka. Koliko je interesantna.
✓ Reč matematika potiče od grčke reči máthēma, koja znači učenje, studije, nauka.
✓ Znate li za izraz diskalkulija? Diskalkulija znači da neko teže uči računanje, što može da bude izraženo kao nemogućnost da razume brjeve ili da nauči činjenice iz matematike.
✓ Zaseci i udubljenja na skeletima životinja dokazuju da su ljudi računali i bavili se matematikom mnogo pre nego što je ona nastala kao nauka, još 30.000 dodina p.n.e.
✓ Broj 5 se na tai jeziku izgovara kao “ha”. Zato se 555 često koristi kao skraćenica u slengu za “hahaha”.
✓ Nula (0) je jedini broj koji ne može da se predstavi rimskim brojevima.
✓ Engleska reč za nulu, zero, nastala je od arapske reči sifr, koja je takođe dala i reč šifra, što znači ”tajni način pisanja”.
✓ Znate li za magiju broja 9? Pomnožite bilo koji broj sa 9 i zatim saberite sve pojedinačne cifre rezultata (proizvoda) dok ne dobijete jednu cifru. Zbir ovih pojedinačnih cifara daće vam 9.
✓ Evo interesantnog načina da proverite deljivost sa brojem 3. Broj je deljiv sa 3 ako je zbir njegovih cifara deljiv sa 3.
✓ Znak jednakosti (=) je izumeo matematičar iz XVI veka, Robert Record, jer mu je dosadilo da piše “je jednako” u jednačinama.
✓ Broj Googol (po kome je pretraživač Google dobio ime, samo sa greškom u spelovanju) koristi se da se izrazi broj 1 praćen sa 100 nula i prvi ga je upotrebio 9-ogodišnjak Milton Sirotta još 1940. godine.
✓ Abakus se smatra direktnim pretkom dgitrona.
✓ 12.345.678.987.654.321 je proizvod brojeva 111.111.111 x 111.111.111. Primećujete da se cifre u broju penju od 1 do 9 i nazad.
✓ Znaci za plus (+) i minus (-) koriste se još od 1489. godine.
✓ Ikosaedar je geometrijski oblik da 20 strana. Koliko god vam to neobično zvučalo, to je jedan od 5 pravilnih poliedara.
✓ Trigonometrija je oblast matematike koja pročuava vezu između uglova trougla i njihovih strana.
✓ Ako sabirate brojeve od 1 do 100 redom, zbir je 5.050. Parovi 1 i 100, 2 i 99, 3 i 98 i tako redom, uvek daju zbor 101. Takvih parova je 50 (100 / 2), dakle, 101 x 50 = 5.050.
✓ 2 i 5 su jedini prosti projevi koji se završavaju sa 2 ili 5.
✓ Trenutak ili momenat je zapravo prava jedinica za vreme koja označava 1/100 deo sekunde.
✓ U grupi od 23-oje ljudi, bar dvoje imaju isti dan rođenja sa verovatnoćom većom od ½.
✓ Ako ima 50 učenika u razredu, gotovo da je sigurno da će dvoje biti rođeni istog dana.
✓ Od svih geometrijskih oblika koji imaju isti obim, krug ima najveću površinu.
✓ Od svih geometrijskih oblika koji imaju istu površninu, krug ima najmanji obim.
✓ U gradu Tajpej, na Tajvanu, građanima je 1995. godine dozvoljeno da uklone cifru 4 iz uličnog broja zato što se izgovara isto kao i reč smrt na kineskom. Zbog toga mnoge bolnice u Kini nemaju 4. sprat.
✓ Grčki matematičar Pitagora je u izračunavanju jednačina koristio malo kamenje. Otuda je ime kalkulator nastalo odgrčke reči za šljunak.
✓ U mnogim kulturama broj 13 smatra se baksuznim i postoji mnogo mitova o tome. Na prmer, u mnogim starim evropskim religijama bilo je 12 dobrig bogova, a loš bog je nazivan 13. bog. Drugo sujeverje potiče od Poslednje večere – bilo je 13 ljudi za trpezom, ukljulujući i Isusa, a Juda se smatra 13. gostom.
✓ Da li ste čuli za Fibonačija i njegov niz? To je niz brojeva u kome je broj zbir brojeva pre njega. Evo, na prmer: 1, 1, 2, 3, 5, 8, 13, 21, 34, i tako dalje.
✓ Da li ste čuli za broj palindrom? To je broj koji se isto čita sa obe strane, na primer: 12421.
✓ Arapski brojevi kao što su 1, 2, 3… nastale su pre više od 1.000 godina.
✓ Broj Pi ne može da se izrazi kao razlomak, što ga čini iracionalnim brojem. Takođe je i beskonačan.
izvor:http://matematika.edu.rs/
✓ Reč matematika potiče od grčke reči máthēma, koja znači učenje, studije, nauka.
✓ Znate li za izraz diskalkulija? Diskalkulija znači da neko teže uči računanje, što može da bude izraženo kao nemogućnost da razume brjeve ili da nauči činjenice iz matematike.
✓ Zaseci i udubljenja na skeletima životinja dokazuju da su ljudi računali i bavili se matematikom mnogo pre nego što je ona nastala kao nauka, još 30.000 dodina p.n.e.
✓ Broj 5 se na tai jeziku izgovara kao “ha”. Zato se 555 često koristi kao skraćenica u slengu za “hahaha”.
✓ Nula (0) je jedini broj koji ne može da se predstavi rimskim brojevima.
✓ Engleska reč za nulu, zero, nastala je od arapske reči sifr, koja je takođe dala i reč šifra, što znači ”tajni način pisanja”.
✓ Znate li za magiju broja 9? Pomnožite bilo koji broj sa 9 i zatim saberite sve pojedinačne cifre rezultata (proizvoda) dok ne dobijete jednu cifru. Zbir ovih pojedinačnih cifara daće vam 9.
✓ Evo interesantnog načina da proverite deljivost sa brojem 3. Broj je deljiv sa 3 ako je zbir njegovih cifara deljiv sa 3.
✓ Znak jednakosti (=) je izumeo matematičar iz XVI veka, Robert Record, jer mu je dosadilo da piše “je jednako” u jednačinama.
✓ Broj Googol (po kome je pretraživač Google dobio ime, samo sa greškom u spelovanju) koristi se da se izrazi broj 1 praćen sa 100 nula i prvi ga je upotrebio 9-ogodišnjak Milton Sirotta još 1940. godine.
✓ Abakus se smatra direktnim pretkom dgitrona.
✓ 12.345.678.987.654.321 je proizvod brojeva 111.111.111 x 111.111.111. Primećujete da se cifre u broju penju od 1 do 9 i nazad.
✓ Znaci za plus (+) i minus (-) koriste se još od 1489. godine.
✓ Ikosaedar je geometrijski oblik da 20 strana. Koliko god vam to neobično zvučalo, to je jedan od 5 pravilnih poliedara.
✓ Trigonometrija je oblast matematike koja pročuava vezu između uglova trougla i njihovih strana.
✓ Ako sabirate brojeve od 1 do 100 redom, zbir je 5.050. Parovi 1 i 100, 2 i 99, 3 i 98 i tako redom, uvek daju zbor 101. Takvih parova je 50 (100 / 2), dakle, 101 x 50 = 5.050.
✓ 2 i 5 su jedini prosti projevi koji se završavaju sa 2 ili 5.
✓ Trenutak ili momenat je zapravo prava jedinica za vreme koja označava 1/100 deo sekunde.
✓ U grupi od 23-oje ljudi, bar dvoje imaju isti dan rođenja sa verovatnoćom većom od ½.
✓ Ako ima 50 učenika u razredu, gotovo da je sigurno da će dvoje biti rođeni istog dana.
✓ Od svih geometrijskih oblika koji imaju isti obim, krug ima najveću površinu.
✓ Od svih geometrijskih oblika koji imaju istu površninu, krug ima najmanji obim.
✓ U gradu Tajpej, na Tajvanu, građanima je 1995. godine dozvoljeno da uklone cifru 4 iz uličnog broja zato što se izgovara isto kao i reč smrt na kineskom. Zbog toga mnoge bolnice u Kini nemaju 4. sprat.
✓ Grčki matematičar Pitagora je u izračunavanju jednačina koristio malo kamenje. Otuda je ime kalkulator nastalo odgrčke reči za šljunak.
✓ U mnogim kulturama broj 13 smatra se baksuznim i postoji mnogo mitova o tome. Na prmer, u mnogim starim evropskim religijama bilo je 12 dobrig bogova, a loš bog je nazivan 13. bog. Drugo sujeverje potiče od Poslednje večere – bilo je 13 ljudi za trpezom, ukljulujući i Isusa, a Juda se smatra 13. gostom.
✓ Da li ste čuli za Fibonačija i njegov niz? To je niz brojeva u kome je broj zbir brojeva pre njega. Evo, na prmer: 1, 1, 2, 3, 5, 8, 13, 21, 34, i tako dalje.
✓ Da li ste čuli za broj palindrom? To je broj koji se isto čita sa obe strane, na primer: 12421.
✓ Arapski brojevi kao što su 1, 2, 3… nastale su pre više od 1.000 godina.
✓ Broj Pi ne može da se izrazi kao razlomak, što ga čini iracionalnim brojem. Takođe je i beskonačan.
izvor:http://matematika.edu.rs/

Mozak nas brani - matematikom
Kada oseti da nam se približava neka opasnost,
naš mozak se okreće - matematici.
Krećete se do rafa sa žitaricama i odjednom čujete zvuk nadolazeće katastrofe. Jedan tinejdžer je kolica svoje mame sa namirnicama usmerio pravo na vas.
U vizuelnom flešu koji imate pre zabijanja kolica u svoje noge, šta vam prolazi kroz glavu? Čista matematika, ili tako bar tvrdi tim američkih i kanadskih istraživača iz Neurološkog instituta u Montrealu i sa Univerziteta u Merilendu. Oni su mapirali vizuelne moždane procese kojim se koristite kako biste zaključili da li će vas udar kolica povrediti. Određeni neuroni koriste se kalkulacijom za izbegavanje nesreće. Podstičući neke moždane regije oni izračunavaju potrebne informacije - koliko je objekat udaljen, da li se bezopasno kreće udesno ili ulevo ili ubrzava? Specijalizovani neuroni u vizuelnom delu moždane kore, u oblasti poznatoj kao MST, detektuju obrasce kretanja, poput ekspanzije, rotacije i deformacije. Proračuni koji se koriste u ovom procesu su ranijeo bili nepoznati – kažu istraživači. Međutim, oni sada znaju kako funkcionišu pojedinačni neuroni u MST. Ali nemojte sebi mnogo davati na zanačaju jer mislite da imate munjevite matematičke reflekse. "U suštini, ovaj proces je sličan onome kroz koji prolazi muva, buba ili ptica,” kaže dr Kristofer Pak o sistemu najviše uzbune koji se pokreće kad osetimo da nam se približava opasnost. On sumnja da se način ovih proračuna mnogo promenio od vremena pećinskih ljudi. Njegov tim je otkrio da se u osnovi ove matematike krije veoma jednostavan proračun koji se svodi na množenje problema.
vest preuzeta sa www.b92.net
Kada oseti da nam se približava neka opasnost,
naš mozak se okreće - matematici.
Krećete se do rafa sa žitaricama i odjednom čujete zvuk nadolazeće katastrofe. Jedan tinejdžer je kolica svoje mame sa namirnicama usmerio pravo na vas.
U vizuelnom flešu koji imate pre zabijanja kolica u svoje noge, šta vam prolazi kroz glavu? Čista matematika, ili tako bar tvrdi tim američkih i kanadskih istraživača iz Neurološkog instituta u Montrealu i sa Univerziteta u Merilendu. Oni su mapirali vizuelne moždane procese kojim se koristite kako biste zaključili da li će vas udar kolica povrediti. Određeni neuroni koriste se kalkulacijom za izbegavanje nesreće. Podstičući neke moždane regije oni izračunavaju potrebne informacije - koliko je objekat udaljen, da li se bezopasno kreće udesno ili ulevo ili ubrzava? Specijalizovani neuroni u vizuelnom delu moždane kore, u oblasti poznatoj kao MST, detektuju obrasce kretanja, poput ekspanzije, rotacije i deformacije. Proračuni koji se koriste u ovom procesu su ranijeo bili nepoznati – kažu istraživači. Međutim, oni sada znaju kako funkcionišu pojedinačni neuroni u MST. Ali nemojte sebi mnogo davati na zanačaju jer mislite da imate munjevite matematičke reflekse. "U suštini, ovaj proces je sličan onome kroz koji prolazi muva, buba ili ptica,” kaže dr Kristofer Pak o sistemu najviše uzbune koji se pokreće kad osetimo da nam se približava opasnost. On sumnja da se način ovih proračuna mnogo promenio od vremena pećinskih ljudi. Njegov tim je otkrio da se u osnovi ove matematike krije veoma jednostavan proračun koji se svodi na množenje problema.
vest preuzeta sa www.b92.net
Matematika može biti i šaljiva
Jednačina 1
čovek = jede + spava + radi + uživa
magarac = jede + spava
Znači:
čovek = magarac + radi + uživa
Odnosno:
čovek - uživa = magarac + radi
Drugim rečima:
čovek koji ne zna kako da uživa = magarac koji radi
Jednačina 2
muškarac = jede + spava + zarađuje novac
magarac = jede + spava
Znači:
muškarac = magarac + zarađuje novac
Odnosno:
muškarac - zarađuje novac = magarac
Drugim rečima:
muškarac koji ne zarađuje novac = magarac
Jednačina 3
žena = jede + spava + troši novac
magarac = jede + spava
Znači:
žena = magarac + troši novac
žena - troši novac = magarac
Drugim rečima:
žena koja ne troši novac = magarac
++++++++++++ +++++++++ +++++++++ +++++++++
Da zaključimo:
Iz jednačine 2 i jednačine 3 jednoznačno sledi:
muškarac koji ne zarađuje novac = žena koja ne troši novac
Znači:
muškarac zarađuje novac da ne bi dozvolio ženi da ispadne magarac,
a žena troši novac da ne bi dozvolila muškarcu da ispadne magarac!
Dakle, imamo:
muškarac + žena = magarac + zarađuje novac + magarac + troši novac
Konačno, iz dosada navedenih jednakosti možemo da izvedemo zaključak:
MUŠKARAC + ŽENA = 2 MAGARCA KOJI SREĆNO ŽIVE ZAJEDNO
izvor:http://ivanaantic.weebly.com/
|
|
|
Reakcija kada pitate mangupe iz posledenje klupe. Da li vam je ovo jasno?
|
|
|
Klikom na sliku ispod otvoriće se dokument u kome možete saznati o poreklu nekih geometrijskih naziva
Pogledajte interesantan crtani film o matematici
Eratosten i bunar
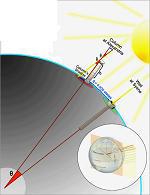
Eratosten iz Kirene (276-194. pne), upravnik Aleksandrijske biblioteke, postao je poznat kao prvi čovjek u istoriji koji je izmjerio obim Zemlje (240. pne). Eratosten je došao do svog otkrića primjenjujući geometriju. Uočio je da u podne, za vrijeme ljetne dugodnevice 21. juna (ljetni solisticij) u gradu Sijeni, predmeti ne bacaju sjenu. Vidio je svoj odraz u jednom dubokom bunaru do čijeg dna sunčevi zraci inače ne dopiru. Za Eratostena je to značilo da štap poboden pod pravim uglom u zemlju stoji uporedo sa sunčevim zracima. On je znao da u Aleksandriji sunce uvijek pravi sjenu i da je Sijena znatno južnije od Aleksandrije.

Takođe je znao za tvrdnje nekih grčkih filozofa da je Zemlja okrugla što mu je sljedeći misaoni eksperiment i potvrdio. Zamislio je polupravu, koja polazi iz središta Zemlje i prolazi kroz tačku koja predstavlja grad Sijenu, paralelnu sa dužima koje predstavljaju sunčeve zrake; i polupravu koja polazi iz središta Zemlje do tačke koja predstavlja grad Aleksandriju a nije paralelna sunčevim zracima. Ona se presjeca sa njima pod određenim uglom, pa se zbog toga javlja sjena. Eratosten je mjerenjem utvrdio da je taj ugao na ljetni solisticij približno iznosio 7,2º što je pedeseti dio od 360º tj. punog ugla. Na osnovu toga je zaključio da je Zemljin obim pedeset puta veći od razdaljine između Sijene i Aleksandrije. Od putnika je saznao da je kamilama potrebno 50 dana da pređu put između ova dva grada i koliko jedna kamila prelazi dnevno. Računom je dobio rastojanje između Sijene i Aleksandrije, ono je iznosilo 5000 stadija. Pomnoživši 5000 stadija sa 50, Eratosten je dobio da obim Zemlje iznosi 250000 stadija.
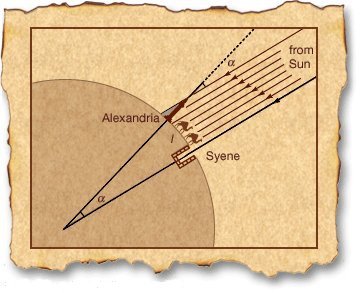
Takođe je znao za tvrdnje nekih grčkih filozofa da je Zemlja okrugla što mu je sljedeći misaoni eksperiment i potvrdio. Zamislio je polupravu, koja polazi iz središta Zemlje i prolazi kroz tačku koja predstavlja grad Sijenu, paralelnu sa dužima koje predstavljaju sunčeve zrake; i polupravu koja polazi iz središta Zemlje do tačke koja predstavlja grad Aleksandriju a nije paralelna sunčevim zracima. Ona se presjeca sa njima pod određenim uglom, pa se zbog toga javlja sjena. Eratosten je mjerenjem utvrdio da je taj ugao na ljetni solisticij približno iznosio 7,2º što je pedeseti dio od 360º tj. punog ugla. Na osnovu toga je zaključio da je Zemljin obim pedeset puta veći od razdaljine između Sijene i Aleksandrije. Od putnika je saznao da je kamilama potrebno 50 dana da pređu put između ova dva grada i koliko jedna kamila prelazi dnevno. Računom je dobio rastojanje između Sijene i Aleksandrije, ono je iznosilo 5000 stadija. Pomnoživši 5000 stadija sa 50, Eratosten je dobio da obim Zemlje iznosi 250000 stadija.
Smatra se da 1 grčki stadij iznosi oko 185 metara a egipatski oko 157.5 metara. Zavisno od toga koju jedinicu mjere je koristio, izračunavamo da je kao vrijednost obima Zemlje dobio 46250 km ili 39375 km (srednji obim zemlje po današnjim saznanjima iznosi 40,030.2 km).
Euklid je dobio da je rastojanje između Sijene (grada Asuana u sadašnjem Egiptu) i Aleksandrije 5000 stadija, tj. 925 km po grčkom sistemu mjera ili 787.5 km po egipatskom. Možemo da vidimo na http://www.wolframalpha.com/ (unesite u polje za pretragu “aswan alexandria“) da je rastojanje između ova dva grada 844 km. Razlika u apsolutnim greškama je 24,5 km (u prvom slučaju je apsolutna greška 81 km a u drugom 56,5 km), tako da je vjerovatnije da je korišten egipatski sistem mjera (precijenili su kamile). U tom slučaju Eratosten je napravio grešku od 1,64%.
izvor:https://zadaci.wordpress.com
Definicije iz prve knjige Euklidovih ,,Elemenata"

Elementi su kapitalno antičko delo o matematici, a za njihovog autora smatra se starogrčki naučnik Euklid, iz 3. veka pre nove ere. Euklidovi Elementi sadrže 13 knjiga i predstavljaju sistematsko izlaganje poznate grčke matematike tog vremena iz oblsti: elementarne geometrije, teorije brojeva, algebre, teorije merenja geometrijskih veličina i elemenata teorije graničnih vrednosti. Jedan su od najvažnijih izvora za Istoriju matematike, a i istoriju civilizacije uopšte.
U prvoj knjizi Elemenata, Euklid daje osnovne geometrijske definicije. Njih ima dvadeset tri, pa navedimo ih.
1. Tačka je ono što nema delova.
2. Linija je dužina bez širine.
3. Krajevi linije su tačke.
4. Prava je linija ona, koja za tačke na njoj podjednako leži.
5. Površina je ono što ima samo dužinu i širinu.
6. Krajevi površine su linije.
7. Ravan je površina koja za prave na njoj podjednako leži.
8. Ugao u ravni je uzajamni nagib dveju linija u ravni koje se seku i koje ne leže
na istoj pravoj.
9. Ako su linije koje obrazuju ugao prave, ugao se zove pravolinijski.
10. Ako prava, koja stoji na drugoj pravoj, obrazuje sa ovom dva susedna jednaka ugla,
savki od njih je prav, a podignuta prava zove se normala na onoj na kojoj stoji.
11. Tup ugao je onaj koji je veći od pravog.
12. Oštar ugao je onaj koji je manji od pravog.
13. Granica je ono što je kraj ma čega.
14. Figura je ono što je omeđeno ili jednom ili sa više granica.
15. Krug je ravna figura omeđena takvom jedinom linijom (koja se zove periferija),
da su sve prave povučene od jedne tačke, koja se nalazi u samoj figuri, prema toj
liniji (prema periferiji kruga) međusobno jednake.
16. Ova tačka zove se središte kruga.
17. Prečnik kruga je svaka prava što prolazi kroz središte kruga a ograničena je
sa svake strane periferijom kruga; on polovi krug.
18. Polukrug je figura ograničena prečnikom i njime odvojenom periferijom
kruga; središte polukruga je isto kao i središte kruga.
19. Pravolinijske figure su one koje su ograničene pravama; trostrane su
ograničene sa tri, četvorostrane sa četiri, mnogostrane sa više od četiri
prave.
20. Od trostranih figura jednakostrani trougao ima tri jednake strane,
jednakokraki ima samo dve jednake strane, a raznostrani ima tri nejednake
strane.
21. Dalje, od trostranih figura je pravougli trougao onaj koji ima prav ugao,
tupougli onaj koji ima tup ugao, a oštrougli koji ima tri oštra ugla.
22. Od četvorostranih figura kvadrat je jednakostran i sa pravim uglovima,
pravougaonik je sa pravim uglovima, no nije sa jednakim stranama, romb sa
jednakim stranama, no nije sa pravim uglovima, romboid sa jednakim
naspramnim stranama, no nije jednakostran ni sa pravim uglovima. Ostale
četvorostane figure neka se zovu trapezi.
23. Paralelne su one prave koje se nalaze u istoj ravni i koje se, produžene u
beskrajnost na obe strane, ne seku jedna sa drugom.
Sadržaje svih 13 knjiga Euklidovih elemenata u prevodu Antona Bilimoviča, možete čitati na ovom linku profesora Matematičkog Fakulteta u Beogradu, Zorana Lučića: http://poincare.matf.bg.ac.rs/nastavno/zlucic
izvor:zadaci.wordpress.com


